Dueling DDQN

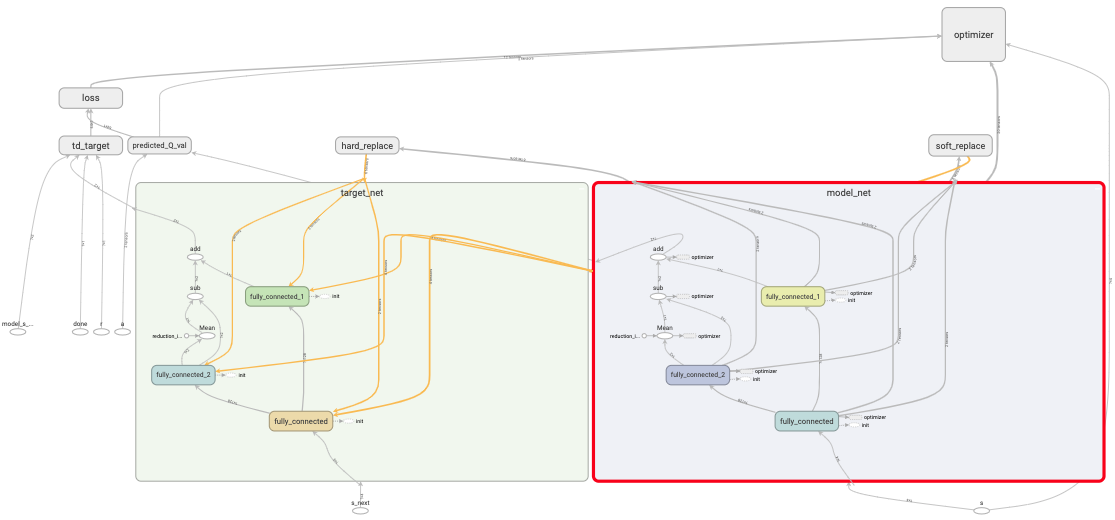
This post documents my implementation of the Dueling Double Deep Q Network (Dueling DDQN) algorithm.

A Dueling Double Deep Q Network (Dueling DDQN) implementation in tensorflow with random experience replay. The code is tested with Gym’s discrete action space environment, CartPole-v0 on Colab.

Code on my Github

If Github is not loading the Jupyter notebook, a known Github issue, click here to view the notebook on Jupyter’s nbviewer.

Notations:

Network = \(Q_{\theta}\)

Parameter = \(\theta\)

Network Q value = \(Q_{\theta}\) (s, a)

Value function = V(s)

Advantage function = A(s, a)

Parameter from the Advantage function layer = \(\alpha\)

Parameter from the Value function layer = \(\beta\)

Equations:

(eqn 9) from the original paper (Wang et al., 2015):

Q(s, a; \(\theta\), \(\alpha\), \(\beta\)) = V(s; \(\theta\), \(\beta\)) \(+\) [ A(s, a; \(\theta\), \(\alpha\)) \(-\) \(\frac{1}{|A|}\) \(\sum_{a'}\) A(s, \(a^{'}\); \(\theta\), \(\alpha\)) ]

Key implementation details:

V represents the value function layer, A represents the Advantage function layer:

# contruct neural network
def built_net(self, var_scope, w_init, b_init, features, num_hidden, num_output):              
    with tf.variable_scope(var_scope):          
      feature_layer = tf.contrib.layers.fully_connected(features, num_hidden,
                                                        activation_fn = tf.nn.relu,
                                                        weights_initializer = w_init,
                                                        biases_initializer = b_init)
      V = tf.contrib.layers.fully_connected(feature_layer, 1,
                                            activation_fn = None,
                                            weights_initializer = w_init,
                                            biases_initializer = b_init)
      A = tf.contrib.layers.fully_connected(feature_layer, num_output,
                                            activation_fn = None,
                                            weights_initializer = w_init,
                                            biases_initializer = b_init)   
      Q_val = V + (A - tf.reduce_mean(A, reduction_indices=1, keepdims=True)) # refer to eqn 9 from the original paper          
    return Q_val

Tensorflow graph:

image

References:

Dueling Network Architectures for Deep Reinforcement Learning (Wang et al., 2015)


2020

PBT for MARL

46 minute read

My attempt to implement a water down version of PBT (Population based training) for MARL (Multi-agent reinforcement learning).

Back to top ↑

2019

.bash_profile for Mac

15 minute read

This post demonstrates how to create customized functions to bundle commands in a .bash_profile file on Mac.

DPPO distributed tensorflow

72 minute read

This post documents my implementation of the Distributed Proximal Policy Optimization (Distributed PPO or DPPO) algorithm. (Distributed continuous version)

A3C distributed tensorflow

27 minute read

This post documents my implementation of the A3C (Asynchronous Advantage Actor Critic) algorithm (Distributed discrete version).

Distributed Tensorflow

78 minute read

This post demonstrates a simple usage example of distributed Tensorflow with Python multiprocessing package.

N-step targets

79 minute read

This post documents my implementation of the N-step Q-values estimation algorithm.

Dueling DDQN with PER

53 minute read

This post documents my implementation of the Dueling Double Deep Q Network with Priority Experience Replay (Duel DDQN with PER) algorithm.

Dueling DDQN

24 minute read

This post documents my implementation of the Dueling Double Deep Q Network (Dueling DDQN) algorithm.

DDQN

29 minute read

This post documents my implementation of the Double Deep Q Network (DDQN) algorithm.

DQN

24 minute read

This post documents my implementation of the Deep Q Network (DQN) algorithm.

Back to top ↑